Do_it_05

Posted Feb 8, 2025

By 윤예진

14 min read

Do_it_05

5.1 버블 정렬

정렬 알고리즘 정의

정렬 알고리즘	정의
버블 (bubble)	데이터의 인접 요소끼리 비교하고, swap 연산을 수행하며 정렬하는 방식
선택 (selection)	대상에서 가장 크거나 작은 데이터를 찾아 선택하는 과정을 반복하면서 정렬하는 방식
삽입 (insertion)	대상을 선택해 정렬된 영역에서 선택 데이터의 적절한 위치를 찾아 삽입하면서 정렬하는 방식
퀵 (quick)	pivot 값을 선정해 해당 값을 기준으로 정렬하는 방식
병합 (merge)	이미 정렬된 부분 집합들을 효율적으로 병합해 전체를 정렬하는 방식
기수 (radix)	데이터의 자릿수를 바탕으로 비교해 데이터를 정렬하는 방식

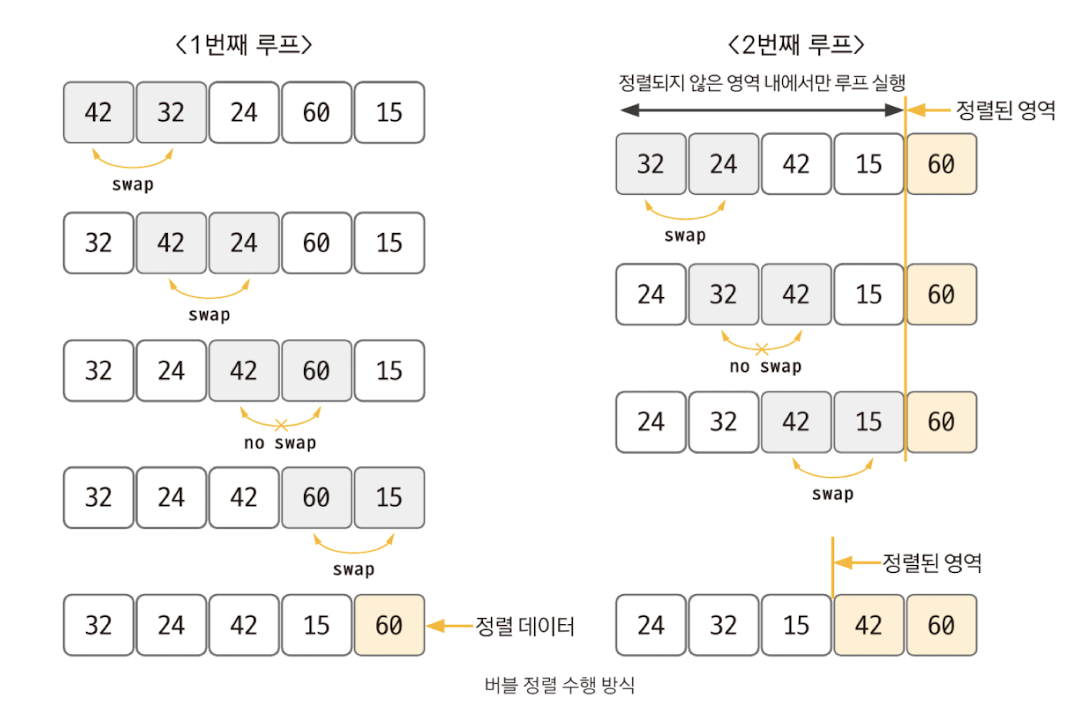
버블 정렬의 핵심 이론

두 인접한 데이터의 크기를 비교해 정렬하는 방법

버블 정렬 과정
1. 비교 연산이 필요한 루프 범위를 설정한다.
2. 인접한 데이터 값을 비교한다.
3. swap 조건에 부합하면 swap 연산을 수행한다.
4. 루프 범위가 끝날 때까지 2~3을 반복한다.
5. 정렬된 영역을 설정한다. 다음 루프를 실행할 때는 이 영역을 제외한다.
6. 비교 대상이 없을 때까지 1~5를 반복한다.

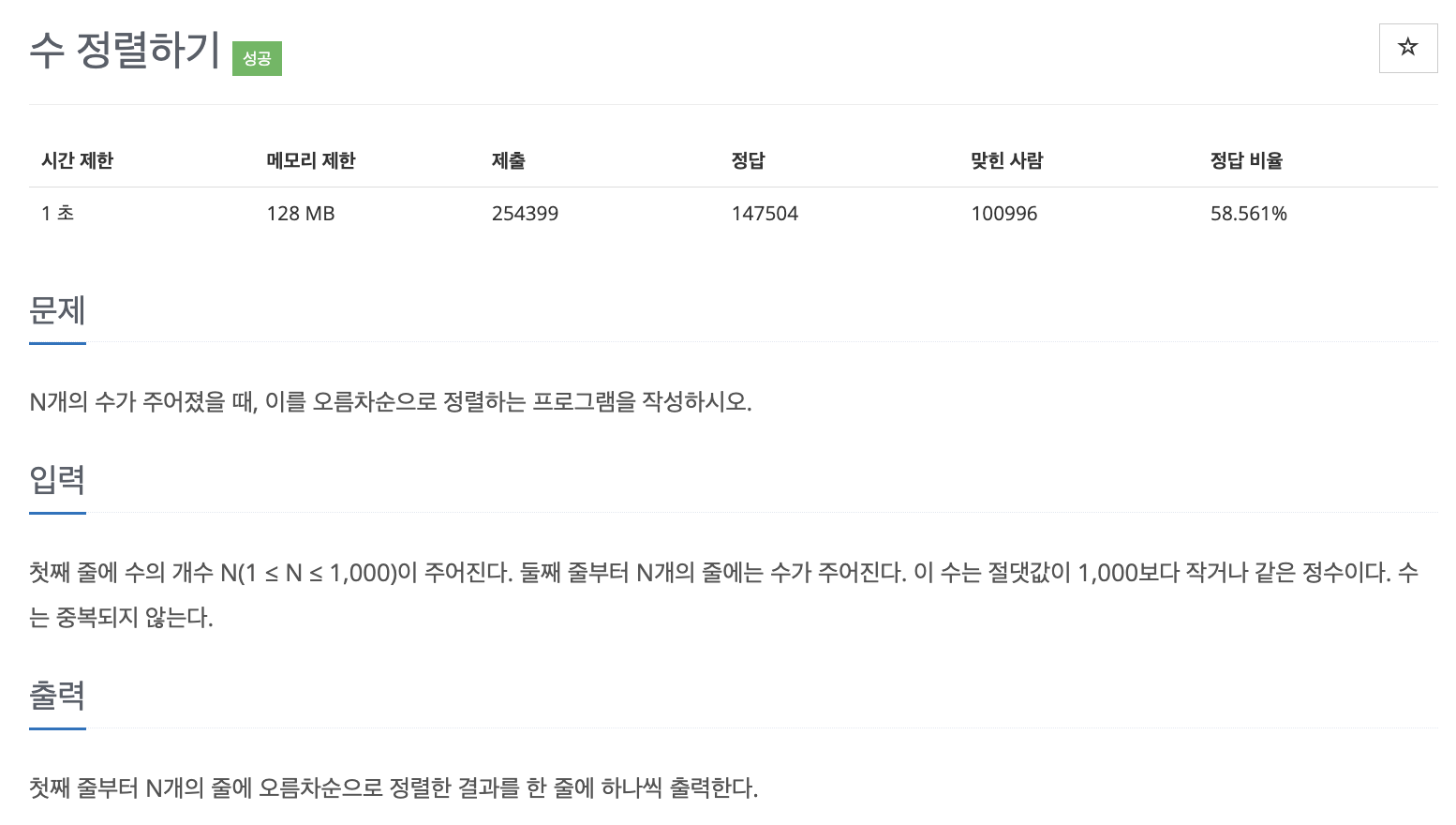
문제 015 : 수 정렬하기 1

풀이

  
import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		int[] arr = new int[N];
		
		for(int i=0; i<N; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
		
		Arrays.sort(arr);
		
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		
		for(int i=0; i<N; i++) {
			bw.write(arr[i]+"\n");
		}
		
		bw.flush();
		bw.close();
	}
}

책에서의 풀이

  
import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		int[] arr = new int[N];
		
		for(int i=0; i<N; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
		
		for (int i=0; i<N-1; i++) {
			for (int j=0; j<N-1-i; j++) {
				if (arr[j] > arr[j+1]) {
					int temp = arr[j];
					arr[j] = arr[j+1];
					arr[j+1] = temp;
				}
			}
		}
		
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		
		for(int i=0; i<N; i++) {
			bw.write(arr[i]+"\n");
		}
		
		bw.flush();
		bw.close();
	}
}

j < N-1-i는 이미 뒤쪽에 정렬된 값(i개)을 다시 비교하지 않기 위해 줄여가는 범위.

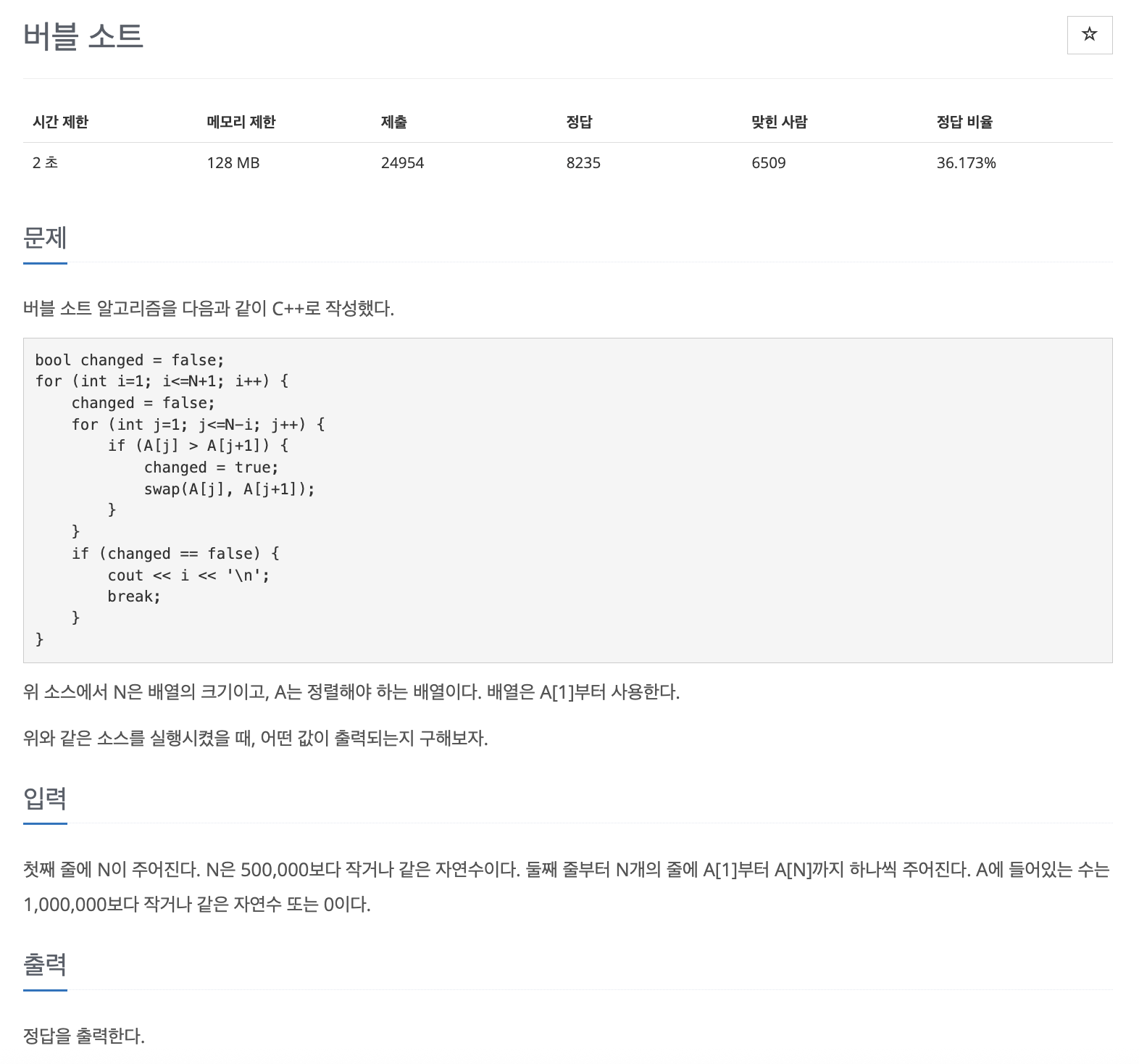
문제 016 : 버블 정렬 프로그램 1

풀이 (틀림)

  
import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		int[] A = new int[N+1];
		boolean change = false;
		for (int i=1; i <= N+1; i++) {
			change = false;
			for (int j=1; j <= N-i; j++) {
				if (A[j] > A[j+1]) {
					change = true;
					int temp = A[j];
					A[j] = A[j+1];
					A[j+1] = temp;
				}
			}
			if (change == false) {
				System.out.println(i);
				break;
			}
		}									
	}
}

문제 분석하기

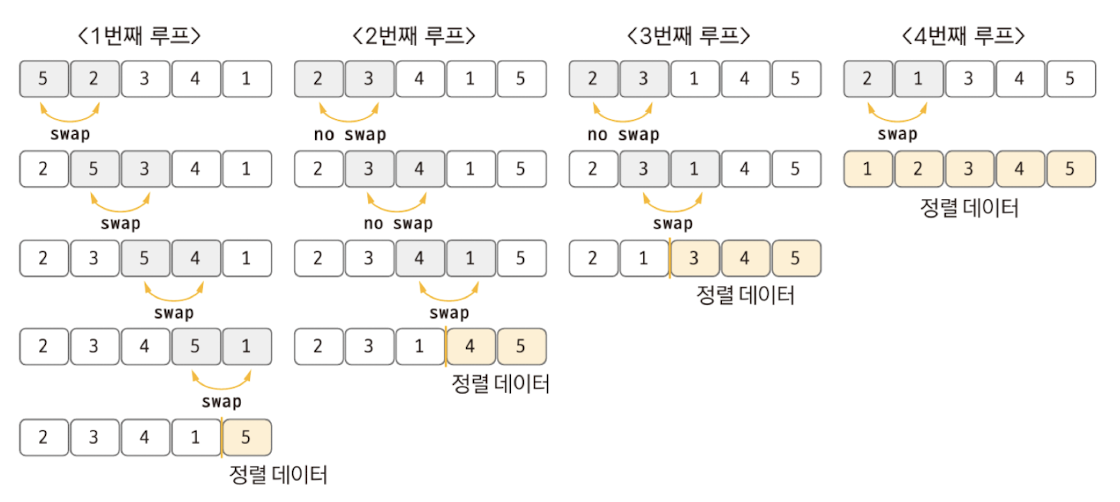
버블 정렬의 swap이 한 번도 일어나지 않은 루프가 언제인지 알아내는 문제
버블 정렬의 이중 for문에서 안쪽 for문 전체를 돌 때 swap이 일어나지 않았다 → 이미 모든 데이터가 정렬됐다
하지만 이 문제는 버블 정렬로 문제를 풀면 시간을 초과할 수 있다. 다른 아이디어 필요
- 안쪽 루프는 1 ~ n-i까지 즉, 왼쪽에서 오른쪽으로 이동하면서 swap을 수행
  - 특정 데이터가 안쪽 루프에서 swap의 왼쪽으로 이동할 수 있는 최대거리가 1이라는 뜻
- 데이터 정렬 전 index와 정렬 후 index를 비교해 가장 많이 이동한 값을 찾으면 된다.

책에서의 문제 풀이

  
public class P1377_버블정렬1 {

    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(reader.readLine());
        mData[] A = new mData[N];

        for (int i = 0; i < N; i++) {
            A[i] = new mData(Integer.parseInt(reader.readLine()), i);
        }

        Arrays.sort(A);   // A 배열 정렬(O(nlogn) 시간 복잡도)

        int Max = 0;
        for (int i = 0; i < N; i++) {
            // 정렬 전 index - 정렬 후 index 계산의 최댓값 저장하기
            if (Max < A[i].index - i)
                Max = A[i].index - i;
        }

        System.out.println(Max + 1);
    }
}

class mData implements Comparable<mData> {
    int value;
    int index;

    public mData(int value, int index) {
        super();
        this.value = value;
        this.index = index;
    }

    @Override
    public int compareTo(mData o) {
        // value 기준 오름차순 정렬하기
        return this.value - o.value;
    }
}

값과 인덱스를 함께 저장한다.
value 기준으로 정렬한다.
원소가 왼쪽으로 몇 칸 이동했는지 (A[i].index - i)
- 음수 → 오른쪽으로 이동 (버블 정렬에 영향 없음)
- 양수 → 왼쪽으로 이동 (중요!)
버블 정렬은 한 번에 왼쪽으로 1칸밖에 못 가기 때문에, 가장 많이 왼쪽으로 이동해야 하는 원소의 이동 횟수가 전체 정렬 횟수를 결정하고, 마지막에 swap이 없는지를 확인하는 pass가 한 번 더 필요해서 +1을 한다.
- 버블 정렬에서 가장 늦게 제자리를 찾는 원소를 구하는 것

5.2 선택 정렬

선택 정렬의 핵심 이론

선택 정렬은 대상 데이터에서 최대나 최소 데이터를 데이터가 나열된 순으로 찾아가며 선택하는 방법
선택 정렬은 구현 방법이 복잡하고, 시간 복잡도도 O(n²)으로 효율적이지 않아 코딩 테스트에서는 많이 사용하지 않는다.

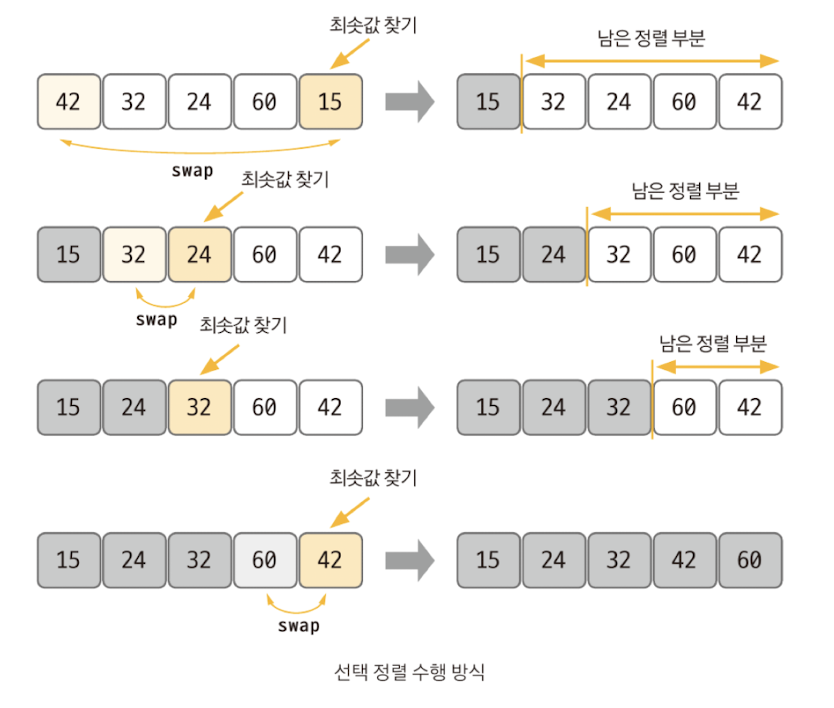
최솟값 또는 최댓값을 찾고, 남은 정렬 부분의 가장 앞에 있는 데이터와 swap하는 것이 선택 정렬의 핵심
선택 정렬 과정 ① 남은 정렬 부분에서 최솟값 또는 최댓값을 찾는다. ② 남은 정렬 부분에서 가장 앞에 있는 데이터와 선택된 데이터를 swap한다. ③ 가장 앞에 있는 데이터의 위치를 변경해(index++) 남은 정렬 부분의 범위를 축소한다. ④ 전체 데이터 크기만큼 index가 커질 때까지, 즉 남은 정렬 부분이 없을 때까지 반복한다.

문제 017 : 내림차순으로 자릿수 정렬하기

풀이

  
import java.io.*;
import java.util.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		String str = br.readLine();
		int len = str.length();
		int[] num = new int[len];
		
		for(int i=0; i<len; i++) {
			num[i] = Integer.parseInt(str.substring(i, i+1));
		}
		
		for(int i=0; i<len; i++) {
			int max = i;
			for (int j=i+1; j<len; j++) { // 최댓값 위치 찾기
				if(num[max] < num[j]) max = j; 
			}
			if (num[i] < num[max]) { // 찾은 최댓값을 현재 자리로 교환
				int temp = num[i];
				num[i] = num[max];
				num[max] = temp;
			}
		}
		
		for(int i=0; i<len; i++) System.out.print(num[i]);
	}
}

오답노트

값이 아니라 index 저장

5.3 삽입 정렬

삽입 정렬의 핵심 이론

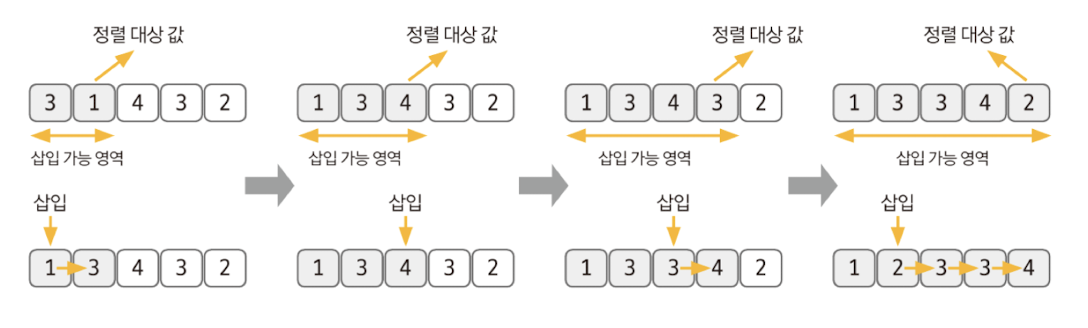
삽입 정렬은 이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입시켜 정렬하는 방식
평균 시간 복잡도는 O(n²)으로 느린 편이지만 구현하기 쉽다.

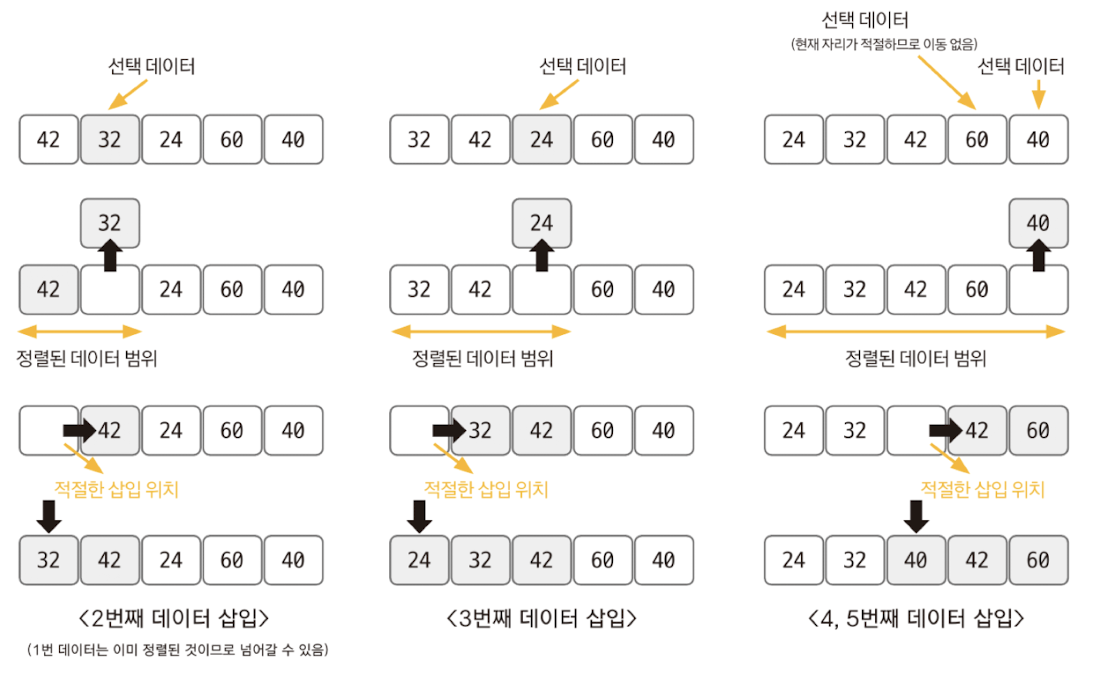
선택된 데이터를 현재 정렬된 데이터 범위 내에서 적절한 위치에 삽입하는 것이 삽입 정렬의 핵심이다.
삽입 정렬 과정 ① 현재 index에 있는 데이터 값을 선택한다. ② 현재 선택한 데이터가 정렬된 데이터 범위에 삽입될 위치를 탐색한다. ③ 삽입 위치부터 index에 있는 위치까지 shift 연산을 수행한다. ④ 삽입 위치에 현재 선택한 데이터를 삽입하고 index++ 연산을 수행한다. ⑤ 전체 데이터의 크기만큼 index가 커질 때까지, 즉 선택할 데이터가 없을 때까지 반복한다.

적절한 삽입 위치를 탐색하는 부분에서 이진 탐색 등과 같은 탐색 알고리즘을 사용하면 시간 복잡도를 줄일 수 있다.

문제 018 : ATM 인출 시간 계산하기

풀이

  
import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine()); // 사람 수
		int[] P = new int[N]; // 사람들이 돈을 인출하는데 걸리는 시간
		
		StringTokenizer st = new StringTokenizer(br.readLine());
		for(int i=0; i<N; i++) {
			P[i] = Integer.parseInt(st.nextToken());
		}
		
		Arrays.sort(P);
		
		
		int sum = P[0];
		int current = P[0];
		for(int i=1; i<N; i++) {
			current += P[i];
			sum += current;
		}
		
		System.out.println(sum);
	}
}

삽입정렬

오답노트

누적합을 또 누적하는 문제 → 누적 시간과 정답을 절대 하나의 변수로 처리하면 안 된다.

책에서의 풀이

  
import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine()); // 사람 수
		int[] P = new int[N]; // 사람들이 돈을 인출하는데 걸리는 시간
		int[] S = new int[N];
		
		StringTokenizer st = new StringTokenizer(br.readLine());
		for(int i=0; i<N; i++) {
			P[i] = Integer.parseInt(st.nextToken());
		}
		
		for(int i=1; i<N; i++) { // 삽입 정렬
			int insert_point=i;
			int insert_value=P[i];
			
			for(int j= i-1; j>= 0; j--) {
				if (P[j] < P[i]) {
            insert_point = j + 1;
            break;
        }
        if (j == 0) {
            insert_point = 0;
        }
	    }
	    
	    for (int j = i; j > insert_point; j--) {
        P[j] = P[j - 1];
		  }
		
		  P[insert_point] = insert_value;
		}

		S[0] = P[0];
		for(int i=1; i<N; i++) {
			S[i] = S[i-1] + P[i];
		}
		int sum = 0;
		for(int i=0; i<N; i++) {
			sum = sum + S[i];
		}
		
		System.out.println(sum);
	}
}

5.4 퀵 정렬

퀵 정렬의 핵심 이론

퀵 정렬은 기준값(pivot)을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬하는 알고리즘.
기준 값을 어떻게 선정하는 지가 시간 복잡도에 많은 영향을 미치는데 평균적인 시간 복잡도는 O(nlogn)이다.

This post is licensed under CC BY 4.0 by the author.

5.1 버블 정렬

버블 정렬의 핵심 이론

문제 015 : 수 정렬하기 1

풀이

책에서의 풀이

문제 016 : 버블 정렬 프로그램 1

풀이 (틀림)

문제 분석하기

책에서의 문제 풀이

5.2 선택 정렬

선택 정렬의 핵심 이론

문제 017 : 내림차순으로 자릿수 정렬하기

풀이

오답노트

5.3 삽입 정렬

삽입 정렬의 핵심 이론

문제 018 : ATM 인출 시간 계산하기

풀이

오답노트

책에서의 풀이

5.4 퀵 정렬

퀵 정렬의 핵심 이론

Trending Tags