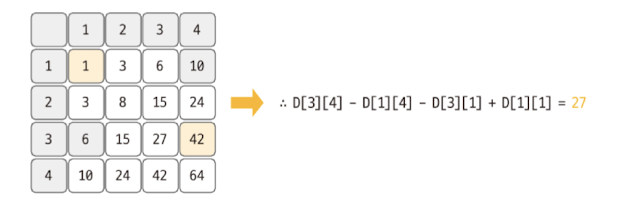4. 자료구조

Posted Feb 1, 2025

By 윤예진

16 min read

4. 자료구조

4.1 배열과 리스트

배열과 리스트의 핵심 이론

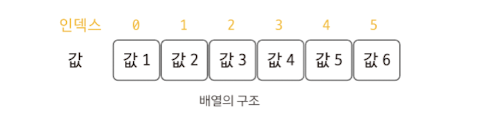
배열

메모리의 연속 공간에 값이 채워져 있는 형태의 자료구조
배열의 값은 인덱스를 통해 참조할 수 있으며, 선언한 자료형의 값만 저장할 수 있다.

배열의 특징

인덱스를 사용하여 값에 바로 접근할 수 있다.
새로운 값을 삽입하거나 특정 인덱스에 있는 값을 삭제하기 어렵다. 값을 삽입하거나 삭제하려면 해당 인덱스 주변에 있는 값을 이동시키는 과정이 필요하다.
배열의 크기는 선언할 때 지정할 수 있으며, 한 번 선언하면 크기를 늘리거나 줄일 수 없다.
구조가 간단하므로 코딩 테스트에서 많이 사용한다.

리스트

값과 포인터를 묶은 노드라는 것을 포인터로 연결한 자료구조
노드는 컴퓨터 과학에서 값과 포인터를 쌍으로 갖는 기초 단위를 부르는 말이다.

리스트의 특징

인덱스가 없으므로 값에 접근하려면 Head 포인터부터 순서대로 접근해야 한다. 다시 말해 값에 접근하는 속도가 느리다.
포인터로 연결되어 있으므로 데이터를 삽입하거나 삭제하는 연산 속도가 빠르다.
선언할 때 크기를 별도로 지정하지 않아도 된다. 다시 말해 리스트의 크기는 정해져 있지 않으며, 크기가 변하기 쉬운 데이터를 다룰 때 적절하다.
포인터를 저장할 공간이 필요하므로 배열보다 구조가 복잡하다.

문제 001 : 숫자의 합 구하기

풀이

  
import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		int N = Integer.parseInt(br.readLine()); // 숫자의 개수
		String str = br.readLine();
		int sum = 0;
		
		for (int i=0; i<N; i++) {
			sum += str.charAt(i) - '0';
		}
		
		System.out.println(sum);
	}
}

오답노트

Integer.parseInt(str.charAt(i)) 는 불가능하다.
- Integer.parseInt()는 String만 받을 수 있다.
- 따라서 이를 해결하기 위한 2가지 방법이 있다.
- 방법1: sum += str.charAt(i) - '0';
  - 아스키 코드 이용하여 문자를 숫자로 변환
- 방법2: sum += Integer.parseInt(String.valueOf(str.charAt(i))); 또는 sum += str.charAt(i) - '0';
  - 문자 → 문자열 → 정수
StringTokenizer st = new StringTokenizer(br.readLine(), "");는 불가능.
- StringTokenizer는 구분자가 반드시 1글자 이상이어야 한다. “”(빈 문자열)는 구분자가 될 수 없다.
- 내부적으로 IllegalArgumentException 또는 NoSuchElementException 문제 발생

책에서의 풀이

  
import java.util.Scanner;

public class P11720_숫자의합 {

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        int N = sc.nextInt();

        // 입력값을 String형 변수 sNum에 저장한 후 char[]형 변수로 변환하기
        String sNum = sc.next();
        char[] cNum = sNum.toCharArray();

        int sum = 0;

        for (int i = 0; i < cNum.length; i++) {
            sum += cNum[i] - '0';   // cNum[i]를 정수형으로 변환하면서 sum에 더하여 누적하기
        }

        System.out.print(sum);
    }
}

팁

자바에서의 형 변환

String형 → 숫자형

  
  String sNum = "1234";   // string형 변수
        
  int i1 = Integer.parseInt(sNum);
  int i2 = Integer.valueOf(sNum);
        
  double d1 = Double.parseDouble(sNum);
  double d2 = Double.valueOf(sNum);
        
  float f1 = Float.parseFloat(sNum);
  float f2 = Float.valueOf(sNum);
        
  long l1 = Long.parseLong(sNum);
  long l2 = Long.valueOf(sNum);
        
  short s1 = Short.parseShort(sNum);
  short s2 = Short.valueOf(sNum);

숫자형 → String형

  
  int i = 1234;
  String i1 = String.valueOf(i);
  String i2 = Integer.toString(i);
        
  double d = 1.23;
  String d1 = String.valueOf(d);
  String d2 = Double.toString(d);
        
  float f = (float) 1.23;
  String f1 = String.valueOf(f);
  String f2 = Float.toString(f);
        
  long l = 1234;
  String l1 = String.valueOf(l);
  String l2 = Long.toString(l);
        
  short s = 1234;
  String s1 = String.valueOf(s);
  String s2 = Short.toString(s);

문제 002 : 평균 구하기

풀이

  
import java.io.*;
import java.util.*;

public class Main {
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		int N = Integer.parseInt(br.readLine());
		int[] score = new int[N];
		double sum = 0;
		
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		for(int i=0; i<N; i++) {
			score[i] = Integer.parseInt(st.nextToken());
		}
		
		Arrays.sort(score);
		int max = score[N-1];
		
		for(int i=0; i<N; i++) {
			sum += (double)score[i]/max*100;
		}
		
		System.out.println(sum/N);
	}
}

오답노트

StringTokenizer 생성 시점 문제
- StringTokenizer를 BufferedReader 생성 후 바로 생성해주었을 때는 런타임 에러가 발생했다.
- 런타임 에러를 일으킨 이유는 입력을 읽는 순서가 잘못되었기 때문이다.
- 토크나이저가 첫 줄(N)을 먼저 읽어버려서 실제 점수 줄을 분해하지 못했고, 그 상태에서 nextToken()을 호출하자 꺼낼 토큰이 없어 에러가 발생했다.
- 즉, StringTokenizer는 생성 시점에 읽은 문자열만 분해하기 때문에 반드시 개수(N)를 먼저 읽고, 그 다음 줄을 토큰화해야 하며, 이 순서가 바뀌면 입력 데이터가 꼬여 런타임 에러가 발생한다.
형변환 주의
- score와 max 모두 int 형이므로, 나누면 몫만 남게됨. 따라서 double형 변환 해야함.

책에서의 풀이

  
public class P1546_평균 {

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();

        int A[] = new int[N];
        for (int i = 0; i < N; i++) {
            A[i] = sc.nextInt();
        }

        long sum = 0;
        long max = 0;

        for (int i = 0; i < N; i++) {
            if (A[i] > max) max = A[i];
            sum = sum + A[i];
        }

        // 한 과목과 관련된 수식을 종합과 관련된 수식으로 변환해 로직이 간단해짐
        System.out.println(sum * 100.0 / max / N);
    }
}

4.2 구간 합

구간 합의 핵심 이론

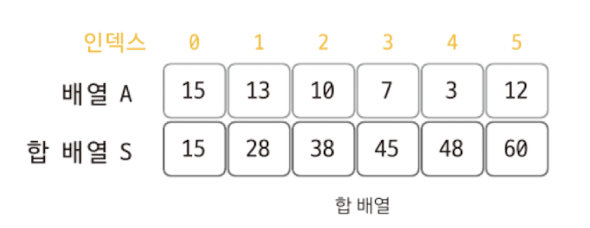
합 배열 S 정의

S[i] = A[0] + A[1] + A[2] + ... A[i-1] + A[i]

합 배열은 기존 배열을 전처리한 배열이라고 생각하면 된다.

이렇게 합 배열을 미리 구해놓으면 기존 배열의 일정 범위 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소한다. 다음 그림을 통해 합 배열을 좀 더 자세히 설명해보겠다.

A[i]부터 A[j]까지의 배열 합을 합 배열 없이 구하는 경우, 최악의 경우는 i가 0이고 j가 N인 경우로 시간 복잡도는 O(N)이다.

이런 경우 앞에서 알아본 합 배열을 사용하면 O(1) 안에 답을 구할 수 있다.

합 배열 S를 만드는 공식

S[i] = S[i-1] + A[i]

이렇게 구현된 합 배열을 이용하여 구간 합 역시 쉽게 구할 수 있다. i에서 j까지 구간 합을 구하는 공식은 다음과 같다.

구간 합을 구하는 공식

S[j] - S[i-1]

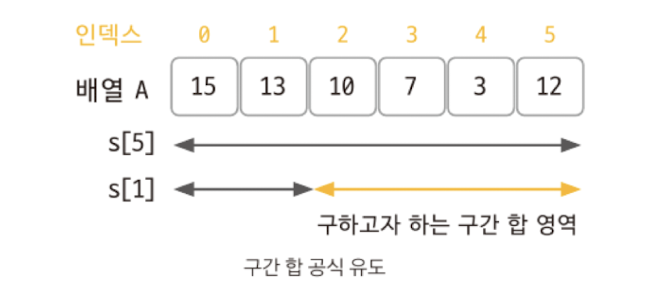
구간 합 공식이 어떻게 나온 것인지 다음 그림을 통해 자세히 알아보겠다.

다음 그림은 배열 A의 A[2]부터 A[5]까지의 구간 합을 합 배열을 통해 구하는 과정을 보여준다.

그림을 보면 합 배열과 구간 합이 연결되어 있다는 것을 알 수 있다. 합 배열만 미리 구현해 두면 구간 합은 한 번의 계산으로 구할 수 있다.

A[2] ~ A[5] 구간 합을 합 배열로 구하는 과정

S[5] = A[0] + A[1] + A[2] + A[3] + A[4] + A[5]

S[1] = A[0] + A[1]

S[5] − S[1] = A[2] + A[3] + A[4] + A[5]

문제 003 : 구간 합 구하기

풀이

  
import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
				
		int N = Integer.parseInt(st.nextToken()); // 개수
		int M = Integer.parseInt(st.nextToken()); // 합을 구해야 하는 횟수
		
		int[] prefix = new int[N+1];
		
		st = new StringTokenizer(br.readLine());
		for(int i=1; i<N; i++) {
			int x = Integer.parseInt(st.nextToken());
			prefix[i] = prefix[i-1]+x; // 1번부터 i번까지의 누적합
		}
		
		StringBuilder sb = new StringBuilder();
		for(int i=0; i<M; i++) {
			st = new StringTokenizer(br.readLine());
			int start = Integer.parseInt(st.nextToken());
			int end = Integer.parseInt(st.nextToken());
			
			int sum = prefix[end] - prefix[start-1];
			sb.append(sum).append('\n');
		}
		
		System.out.println(sb.toString());
	}
}			

오답노트

StringTokenizer 생성 시점

  
  st = new StringTokenizer(br.readLine());
    
  for (int i = 0; i < M; i++) {
      start = Integer.parseInt(st.nextToken());
      end = Integer.parseInt(st.nextToken());
  }

질의는 M줄로 입력되는데 StringTokenizer를 한 번만 생성함 → 다음 질의에서 읽을 토큰이 없어짐
입력 한 줄 = StringTokenizer 한 번 생성

StringBuilder
- 한번에 출력하기 위해

sum 선언위치

  
  int sum = 0;
    
  for (int i = 0; i < M; i++) {
      // sum 초기화 없음
  }

이전 구간합 결과가 다음 계산에 누적됨
질의 간 값이 섞임

구간합 공식 활용 못함
- 배열 초기화 값 0이다.
- 숫자 N개가 주어진다.
- M번 동안 start ~ end 구간의 합을 구해야 한다.
- int sum = prefix[end] - prefix[start - 1]; 이용

책에서의 풀이

  
public class P11659_구간합구하기 {
	public static void main(String[] args) throws IOException {
		BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());

    int suNo = Integer.parseInt(stringTokenizer.nextToken());
    int quizNo = Integer.parseInt(stringTokenizer.nextToken());

    long[] S = new long[suNo + 1];

    stringTokenizer = new StringTokenizer(bufferedReader.readLine());

    for (int i = 1; i <= suNo; i++) {
	    S[i] = S[i - 1] + Integer.parseInt(stringTokenizer.nextToken());
    }

    for (int q = 0; q < quizNo; q++) {
			stringTokenizer = new StringTokenizer(bufferedReader.readLine());

			int i = Integer.parseInt(stringTokenizer.nextToken());
      int j = Integer.parseInt(stringTokenizer.nextToken());

      System.out.println(S[j] - S[i - 1]);
    }
	}
}

문제 004 : 구간 합 구하기 2

풀이

  
import java.util.*;
import java.io.*;

public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		int N = Integer.parseInt(st.nextToken()); // 표의 크기
		int M = Integer.parseInt(st.nextToken()); // 합을 구해야 하는 개수
		int[][] matrix = new int[N+1][N+1];
		
		for(int i=1; i<=N; i++) {
			st = new StringTokenizer(br.readLine());
			for(int j=1; j<=N; j++) {
				matrix[i][j] = matrix[i][j-1] + Integer.parseInt(st.nextToken());
			}
		}
		
		StringBuilder sb = new StringBuilder();
		for(int i=0; i<M; i++) {
			st = new StringTokenizer(br.readLine());
			int x1 = Integer.parseInt(st.nextToken());
			int y1 = Integer.parseInt(st.nextToken());
			int x2 = Integer.parseInt(st.nextToken());
			int y2 = Integer.parseInt(st.nextToken());
			
			long sum = 0;
			for(int j=x1; j<=x2; j++) {
				sum += matrix[j][y2] - matrix[j][y1-1];
			}
			
			sb.append(sum).append('\n');
		}
		
		System.out.println(sb.toString());
	}
}

오답노트

배열 행과 열
- arr[세로][가로]
- 수학 좌표계와 헷갈렸는데, y가 가로를 나타내는 것.

책에서의 풀이

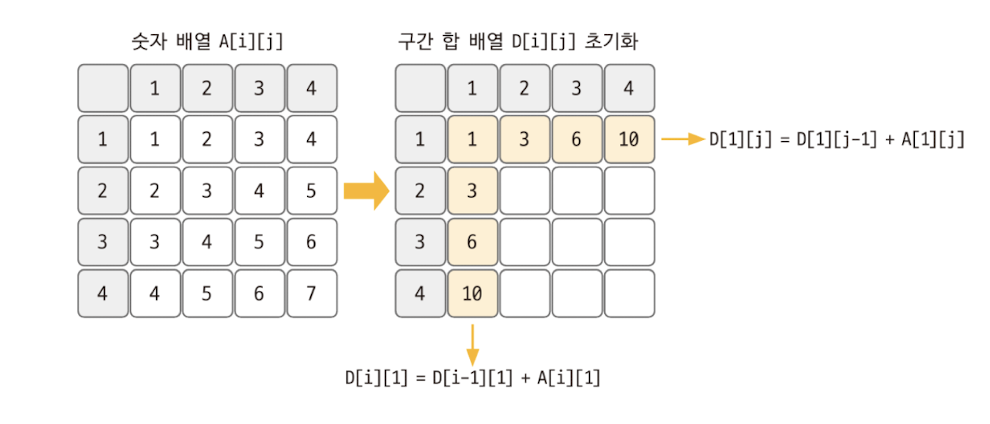
2차원 구간 합 배열 D[X][Y] 정의
- D[X][Y] = 원본 배열의 (0, 0)부터 (X, Y)까지의 사각형 안에 있는 수의 합
D[i][j]의 값을 채우는 구간 합 공식
- D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
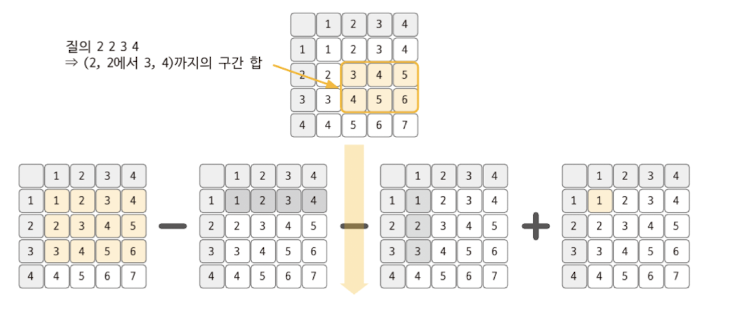
- 예를 들어 질의가 2 2 3 4라면, (3, 4) 구간 합에서 (1, 4) 구간 합, (3, 1) 구간 합을 뺀 다음 중복하여 뺀 (1, 1) 구간 합을 더하면 된다.
- 원본 배열에 표시한 구간 합을 다시 구간 합 배열에 표시하면 다음과 같다.

  
public class P11660_구간합구하기2 {
    public static void main(String[] args) throws Exception {

        BufferedReader br =
                new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int A[][] = new int[N + 1][N + 1];

        for (int i = 1; i <= N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 1; j <= N; j++) {
                A[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        int D[][] = new int[N + 1][N + 1];

        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                // 구간 합 구하기
                D[i][j] = D[i][j - 1]
                        + D[i - 1][j]
                        - D[i - 1][j - 1]
                        + A[i][j];
            }
        }

        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());

            int x1 = Integer.parseInt(st.nextToken());
            int y1 = Integer.parseInt(st.nextToken());
            int x2 = Integer.parseInt(st.nextToken());
            int y2 = Integer.parseInt(st.nextToken());

            // 구간 합 배열로 질의에 답변하기
            int result =
                    D[x2][y2]
                  - D[x1 - 1][y2]
                  - D[x2][y1 - 1]
                  + D[x1 - 1][y1 - 1];

            System.out.println(result);
        }
    }
}

문제 005 : 나머지 합 구하기

알고리즘, Do it! 알고리즘 코딩테스트 자바

알고리즘 코딩테스트

This post is licensed under CC BY 4.0 by the author.

4.1 배열과 리스트

배열과 리스트의 핵심 이론

배열

리스트

문제 001 : 숫자의 합 구하기

풀이

오답노트

책에서의 풀이

팁

문제 002 : 평균 구하기

풀이

오답노트

책에서의 풀이

4.2 구간 합

구간 합의 핵심 이론

합 배열 S 정의

합 배열 S를 만드는 공식

구간 합을 구하는 공식

A[2] ~ A[5] 구간 합을 합 배열로 구하는 과정

문제 003 : 구간 합 구하기

풀이

오답노트

책에서의 풀이

문제 004 : 구간 합 구하기 2

풀이

오답노트

책에서의 풀이

문제 005 : 나머지 합 구하기

Trending Tags