3. 미리 보는 코딩테스트 오답노트
3.1 예상치 못한 음수 결과 해결하기
- 문제를 해결하는 과정에서 예상치 못한 음수 결과 발생 → 자료형을 변경하여 문제를 재검토
- int 보다는 long을 사용하는 것이 더 안전하다.
3.2 시간 초과의 원인을 찾아 해결하기
- 풀이 로직의 시간 복잡도가 제한 시간 안에 문제를 해결할 수 있는 수준인지 확인한다.
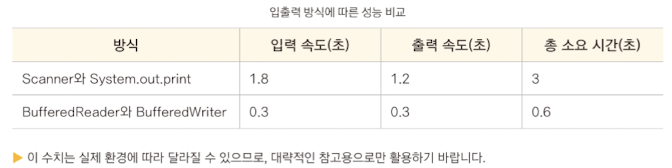
- 입력과 출력 방식부터 최적화할 수 있는지 점검하기 (입력과 출력의 양이 많아질수록 영향 큼)
- Scanner와 System.out.print → BufferedReader, BufferedWriter
- 왜 이런 현상이 발생할까?
- Scanner: 입력할 때마다 필요한 자료형으로 변환하는 과정을 거치므로 처리 속도가 느릴 수 있다.
- System.out.println: 출력이 발생할 때마다 버퍼를 비우는 작업이 이뤄지므로 성능이 저하될 수 있다.
- BufferedReader: 입력을 버퍼에 저장한 후 데이터를 한 번에 읽어오는 방식으로 I/O 작업 횟수를 줄여 성능을 향상한다.
- BufferedWriter:
- 출력할 데이터를 먼저 버퍼에 저장한 후 한 번에 출력하는 방식으로 성능을 개선한다.
- writer() 함수로 데이터를 버퍼에 추가하고, flush() 함수로 버퍼의 내용을 한꺼번에 출력함으로써 효율을 높인다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import java.io.*;
import java.uitl.Scanner;
public class Main {
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int a = sc.nextInt();
System.out.println(a);
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int b = Integer.parseInt(br.readLine());
bw.write(String.valueOf(b));
bw.flush();
}
}
3.3 인덱스에 의미 부여하여 풀어보기
코딩 테스트에서 가장 많이 사용하는 자료구조는 배열이다. 보통 배열을 사용할 때는 인덱스로 데이터에 접근한다. 인덱스는 일반적으로 ‘몇 번째 데이터인지’ 나타내는 역할을 한다. 하지만 상황에 따라 인덱스에 해싱 개념을 적용하여 단순한 위치가 아니라 특정한 의미를 지닌 값으로 활용하면 문제를 더 쉽게 해결할 수 있다.
3.3.1 A[1]의 의미
- 몇 번째 데이터인지 순서를 의미하는 경우 → 첫 번째 데이터를 저장한다.
- 숫잣값으로 의미를 부여한 경우 → 1이라는 값이 몇 개 있는지를 저장한다.
그럼 이제 인덱스에 숫잣값으로 의미를 부여할 때 유리한 상황을 가정해 보겠다.
예를 들어 1000보다 작은 자연수 10,000,000개를 1초 안에 정렬해야 하는 상황이 생겼다고 하자. 데이터의 양이 많아서 일반적인 방법으로는 1초 안에 정렬하기 어렵다. 하지만 인덱스를 값 자체로 활용하면 계수 정렬과 같은 방식으로 제한 시간 내에 정렬할 수 있다. 다음은 데이터를 입력받아 계수 정렬을 이용해 정렬하고 결과를 출력하는 예시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import java.io.*;
import java.util.StringTokenizer;
public class indexHash {
public static void main(String[] args) throws IOException {
BufferedReader br = new BuffereadReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N = Interger.parseInt(br.readLine());
int[] count = new int[1001];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i = 0; i < N; i++) {
int number = Integer.parseInt(st.nextToken());
count[number]++; // 인덱스에 숫자값으로 의미를 부여하여 데이터 저장
}
br.close();
for(int i = 0; i <= 1000; i++) {
if (count[i] != 0) {
for (int j = 0; j < count[i]; j++) {
bw.write(i + " ");
}
}
}
bw.flush();
bw.close();
}
}
여기서 count 배열의 인덱스에 숫잣값으로 의미를 부여함으로써 정렬 속도를 크게 향상했다. 이렇게 하면 10,000,000개의 데이터를 1초 안에 정렬할 수 있다. 계수 정렬은 인덱스에 의미를 부여하는 좋은 예다. 이처럼 인덱스에 의미를 부여하는 해싱 기법은 알고리즘으로 잘 체계화되어 활용되기도 한다. 하지만 실제 코딩 테스트에서는 요구사항에 따라 인덱스에 적절한 의미를 직접 부여해야 하는 문제도 자주 출제된다. 따라서 인덱스를 단순히 ‘몇 번째 순서’로만 생각하지 말고, 문제 상황에 따라 다양한 의미로 변환해 보는 연습이 중요하다.
3.4 나머지 연산의 중요성 알아보기
3.4.1 나머지 연산의 분배 법칙
- 다음과 같이 나머지 연산은 나눗셈을 제외하고 덧셈, 뺄셈, 곱셈의 분배 법칙이 성립한다.
- 예시 값: A = 20, B = 6, C = 3
덧셈의 분배 법칙 성립 →
(A+B) % C = (A%C + B%C) % C1 2
(20+6) % 3 = 26 % 3 = 2 (20%3 + 6%3) % 3 = (2+0) % 3 = 2
뺄셈의 분배 법칙 성립 →
(A-B) % C = (A%C - B%C) % C1 2
(20-6) % 3 = 14 % 3 = 2 (20%3 - 6%3) % 3 = (2-0) % 3 = 2
곱셈의 분배 법칙 성립 →
(A*B) % C = (A%C * B%C) % C1 2
(20*6) % 3 = 120 % 3 = 0 (20%3) * (6%3) % 3 = (2*0) % 3 = 0
나눗셈의 분배 법칙은 성립하지 않음 →
(A/B) % C != (A%C) / (B%C) % C1 2
(20/6) % 3 = 3 % 3 = 0 (20%3) / (2%3) % 3 = (2/2) % 3 = 1
이는 문제를 구현할 때 덧셈, 뺄셈, 곱셈을 모두 계산한 후에 나머지 연산을 한 번만 수행하는 것이 아니라, 로직의 중간 과정마다 나머지 연산을 지속적으로 수행함으로써 자료형의 표현 범위를 초과하지 않도록 설계할 수 있다는 의미다.
예를 들어, 1부터 50까지 곱한 값을 10007로 나눈 나머지를 구하시오. 라는 문제가 있다면 먼저 다음과 같이 시도해볼 수 있다.
1
2
3
4
5
6
7
8
9
public class MOD {
public static void main(String[] args) throws Exception {
long answer = 1;
for (int i=1; i<=50; i++) {
answer = answer*i;
}
System.out.println(answer%10007);
}
}
위를 실행시켜보면, 자연수의 곱을 계산하고 나머지를 구했는데 의도치 않게 음수가 출력되었다. 이는 자료형의 사용 문제이거나 로직의 문제일 수 있다.
로직을 살펴보면, 모든 값을 곱한 후 마지막에 나머지 연산을 수행하고 있다. 이 때문에 곱셈 과정에서 이미 long 자료형의 표현 범위를 초과하여 잘못된 값이 나오는 것이다.
이 문제는 나머지 연산에서 곱셈의 분배 법칙이 성립한다는 점을 활용하여 해결할 수 있다. 즉, 모든 값을 곱한 뒤 마지막에 나머지 연산을 한 번만 적용하는 것과 곱셈을 수행할 때마다 나머지 연산을 적용하는 것이 동일한 결과를 낳는다. 이 원리를 바탕으로 코드를 수정하면 다음과 같다.
1
2
3
4
5
6
7
8
9
public class MOD {
public static void main(String[] args) throws Exception {
long answer = 1;
for (int i=1; i<=50; i++) {
answer = (answer*i)%10007; // 곱셈을 수행할 때마다 나머지 연산을 수행하는 로직
}
System.out.println(answer%10007);
}
}
이와 같이 곱셈을 실행할 때마다 나머지 연산을 함께 수행하도록 코드를 수정하면, 결괏값이 정상적으로 출력되는 것을 확인할 수 있다.
일반적으로 문제에 ‘결괏값을 OO으로 나눈 나머지를 출력하세요.’라는 문구가 있을 경우, 정답을 구한 후 마지막에 나머지 연산을 한 번만 적용하는 방법은 위험할 수 있다. 수행하는 과정마다 나머지 연산을 적용하여 자료형의 표현 범위를 초과하지 않도록 구현해야 한다.
3.5 정렬 기초 다지기
3.5.1 오름차순 정렬
자바에서는
Arrays.sort()함수를 사용하여 오름차순 정렬을 간단하게 구현할 수 있다.1 2 3 4 5 6 7 8
import java.util.Arrays; public class AscendingSort { public static void main(String[] args) { int[] A = {5,3,2,4,1}; Arrays.sort(A); // 오름차순 정렬 System.out.println(Arrays.toString(A)); } }
3.5.2 내림차순 정렬
1
2
3
4
5
6
7
8
9
10
import java.util.Arrays;
import java.util.Collections;
public class DescendingSort1 {
public static void main(String[] args) {
**Integer[]** A = {5, 3, 2, 4, 1};
**Arrays.sort(A, Collections.reverseOrder()); // 내림차순 정렬**
System.out.println(Arrays.toString(A));
}
}
이처럼 배열을 클래스형으로 선언하면 Collections.reverseOrder()를 이용하여 정렬 기준을 지정할 수 있다.
하지만 코딩테스트에서는 클래스형을 배열의 자료형으로 사용하는 경우가 많지 않으므로, 다른 방법도 고려해야 한다.
여기서는 부호를 임시로 반전시키는 아이디어를 활용하여 내림차순 정렬을 구현해보겠다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import java.util.Arrays;
public class DescendingSort2 {
public static void main(String[] args) {
int[] A = {5, 3, 2, 4, 1};
negate(A); // 부호 반전
Arrays.sort(A);
negate(A); // 부호 반전
System.out.println(Arrays.toString(A));
}
static void negate(int[] temp) {
for(int i=0; i<temp.length; i++){
temp[i]*=-1;
}
}
}
3.6 다중 조건 정렬 익히기
여러 기준에 따라 데이터를 정렬해야 하는 상황에는 다중 조건 정렬을 사용하면, 여러 기준을 동시에 적용하여 원하는 순서대로 정렬할 수 있다. 자바에서는 Comparable과 Comparator 인터페이스를 사용하여 다중 조건 정렬을 구현할 수 있다.
3.6.1 Comparable 인터페이스
다음은 Comparable 인터페이스를 사용하여 성적을 정렬한 예시다. 영어 점수를 우선 기준으로 하고, 영어 점수가 같을 경우 수학 점수로 정렬하도록 구현했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Score implements Comparable<Score> {
int english;
int math;
public Score(int english, int math) {
this.english = english;
this.math = math;
}
@Override
public String toString() {
return "Score{" + "english=" + english + ", math=" + math + "}";
}
@Override
// Comparable 인터페이스의 compareTo() 함수를 정렬 기준에 따라 구현
public int compareTo(Score o) {
if (this.english == o.english) return o.math - this.math;
return o.english - this.english;
}
}
Comparable 인터페이스가 뭐야?
→ 객체 자기 자신(this)과 다른 객체(o)를 비교하는 규칙을 제공하는 인터페이스
CompareTo의 리턴값 규칙
- 음수: this가 앞에 옴
- 0: 순서 변화 없음
- 양수: this가 뒤에 옴
따라서, 오름차순으로 정렬하고 싶으면
this-o, 내림차순으로 정렬하고 싶으면o-this를 하면 된다.이 개념이 조금 헷갈렸는데, 예시를 들어보면 쉽게 이해할 수 있다.
- this = 3, o = 5일 때
this-o: 음수 → this가 앞에 옴 → 3, 5 순으로 오름차순o-this: 양수 → this가 뒤에 옴 → 5, 3 순으로 내림차순- this = 5, o = 3일 때
this-o: 양수 → this가 뒤에 옴 → 3, 5 순으로 오름차순o-this: 음수 → this가 앞에 옴 → 5, 3 순으로 내림차순
이제 해당 클래스를 사용하는 클라이언트 코드를 작성해보겠다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import java.util.ArrayList;
import java.util.Collections;
public class Main {
public static void main(String[] args) {
ArrayList<Score> myarr = new ArrayList<>();
myarr.add(new Score(80, 100));
myarr.add(new Score(100, 50));
myarr.add(new Score(70, 100));
myarr.add(new Score(80, 90));
Collections.sort(myarr);
for(Score s : myarr) {
System.out.println(s.toString());
}
}
}
3.6.2 Comparator 인터페이스
수학 점수를 기준으로, 수학 점수가 같을 경우 영어 점수로 정렬해보겠다.
1
2
3
4
5
6
7
8
9
10
11
12
import java.util.Comparator;
public class ScoreComparator implements Comparator<Score> {
@Override
public int compare(Score o1, Score o2) {
// Comparator 인터페이스의 compare() 함수로 정렬 기준에 따라 구현
// 음수: 앞, 양수: 뒤
if (o1.math == o2.math) return o2.english - o1.english;
return o2.math - o1.math;
}
}
클라이언트 코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import java.util.ArrayList;
import java.util.Collections;
public class Main {
public static void main(String[] args) {
ArrayList<Score> myarr = new ArrayList<>();
myarr.add(new Score(80, 100));
myarr.add(new Score(100, 50));
myarr.add(new Score(70, 100));
myarr.add(new Score(80, 90));
Collections.sort(myarr, new ScoreComparator());
// myarr 리스트를 ScoreComparator 기준으로 정렬
// 비교할 땐, ScoreComparator 규칙을 쓰도록.
for (Score s : myarr) {
System.out.println(s.toString());
}
}
}
지금까지 다중 조건 정렬을 구현할 때 가장 일반적으로 사용하는 Comparable과 Comparator 인터페이스의 사용법을 알아보았다. 두 인터페이스 모두 다중 조건 정렬에 활용할 수 있지만, 사용 방식과 유연성에는 다음과 같은 차이가 있다.
| 인터페이스 | 정렬 기준 구현 위치 | 사용 유연성 |
|---|---|---|
| Comparable | 정렬 대상 클래스 내부 | 한 클래스당 하나의 정렬 기준만 정의할 수 있음 |
| Comparator | 클래스 외부 별도 정의 | 한 클래스에 여러 개의 정렬 기준을 정의할 수 있음 |
3.7 이차원 ArrayList 이용한 그래프 구현
1단계: 이차원 ArrayList 선언과 초기화
다음은 그래프의 엣지를 표현하는 클래스다.
1
2
3
4
class Edge {
int endNode;
int value;
}
해당 클래스를 자료형으로 하는 이차원 ArrayList를 초기화하는 방법을 확인해 보겠다.
1
ArrayList<Edge> list[] = new ArrayList[10];
크기가 10이고 자료형이 ArrayList인 배열을 선언한 코드다. 보통 이렇게 선언하면 초기화가 완료되었다고 착각하는 경우가 있다.
하지만 아직 10개의 ArrayList 각각에 대해 객체 생성(메모리 할당)을 추가로 해야 한다.
1
2
3
for (int i = 0; i < 10; i++) {
list[i] = new ArrayList<Edge>();
}
왜 굳이 이렇게 해?
그래프를 저장하는 방법은 크게 2가지다.
(1) 인접 행렬 (2차원 배열)
int[][] graph = new int[N+1][N+1]- 모든 노드 쌍을 저장해야 해서 공간이 큼 (N이 크면 터짐)
(2) 인접 리스트 (이차원 ArrayList)
- 간선이 있는 것만 저장
- 간선이 적을수록 훨씬 효율적
- 코딩테스트에서 거의 이걸 많이 씀
Edge 클래스는 왜 필요해?
- 문제에 가중치가 존재하기 때문이다. (예:
1 -> 2 (비용 4))- 1번 노드에서 출발하는 간선에는 도착 노드(endNode), 비용(value) 두 개를 같이 저장해야 한다. 그래서 간선을 객체로 만들어두는 것이다.
2단계: 그래프 데이터 저장하기
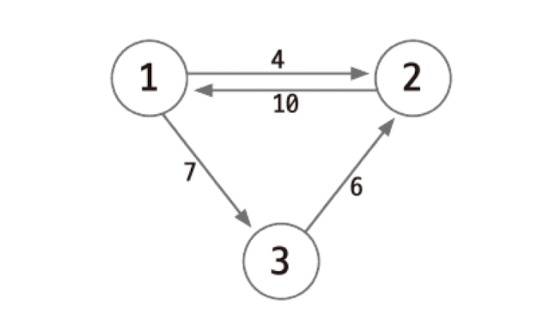
다음과 같이 간단한 그래프가 있다고 가정하겠다.
1
2
3
4
5
3 4 // 노드 3개, 엣지 4개인 그래프
1 2 4 // 1번 노드에서 2번 노드로 가는 가중치 4의 엣지 존재
2 1 10
1 3 7
3 2 6
이러한 그래프 데이터를 이차원 ArrayList 자료구조를 이용하여 저장해 보겠다.
1
2
3
4
5
6
7
8
9
for (int i = 0; i < E; i++) { // 저장할 엣지의 개수만큼 반복
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
list[s].add(new Edge(e, v)); // 이차원 ArrayList에 저장
}
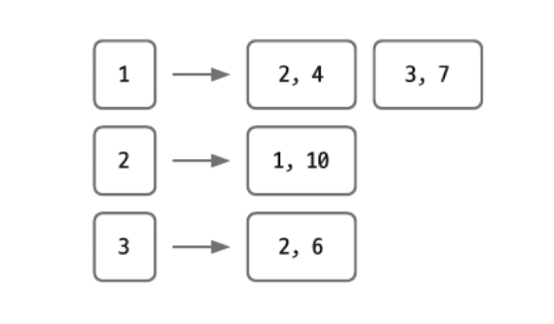
이렇게 저장하면 실제 이차원 ArrayList에는 다음과 같이 데이터가 저장된다.
3단계: 그래프 데이터 가져오기
이제 그래프 데이터 저장까지 완료했다. 마지막으로 필요한 데이터를 가져오는 코드를 살펴보겠다.
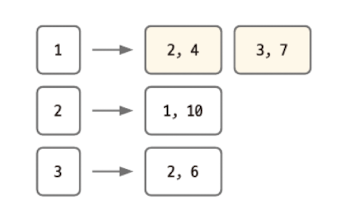
다음은 1번 노드에서 시작되는 엣지 데이터를 가져오는 코드다.
1
2
3
4
5
6
for (int i = 0; i < list[1].size(); i++) {
Edge tmp = list[1].get(i);
int next = tmp.endNode;
int value = tmp.value;
}
이 코드를 사용하면 예제 그래프 데이터에서 다음과 같은 2개의 엣지 데이터를 가져올 수 있다.